Rebus No. 164 (7)

Λύση

Βεραμάν* [Βε(βε)(Bébé**)ραμαν(Sir Chandrasekhara Venkata Raman***)] *Απόχρωση του πράσινου χρώματος. **Tiago Manuel Correia Dias, γνωστό με το ψευδώνυμο Bébé. Γεννήθηκε στην Loures της Πορτογαλίας στις 12 – Ιουλίου – 1990. Είναι ποδοσφαιριστής της Manchester United.. ***Ο Σερ Τσαντρασεκάρα Βενκάτα Ράμαν (Sir Chandrasekhara Venkata Raman), (7 Νοεμβρίου 1888 – 21 Νοεμβρίου 1970) ήταν Ινδός φυσικός, στον οποίο το 1930 απονεμήθηκε το βραβείο Νόμπελ φυσικής για τις εργασίες του σχετικά με τη σκέδαση του φωτός, και ειδικότερα της μερικής μεταβολής του μήκους κύματος μονοχρωματικού φωτός όταν διέρχεται από διαφανές μέσο, καλούμενο φαινόμενο Ράμαν επί τη βάση του οποίου εφαρμόζεται σήμερα και η ομώνυμη τεχνική, φασμα-τοσκοπία Ράμαν.

Γάτα Εναντίων Ποντικιών

Μια γάτα ήταν πολύ καλή στο να πιάνει ποντίκια. Την πρώτη ημέρα έπιασε το ένα τρίτο των ποντικιών. Την δεύτερη ημέρα έπιασε το ένα τρίτο των ποντικιών που είχαν μείνει από τη πρώτη ημέρα. Την τρίτη ημέρα έπιασε το ένα τρίτο των ποντικών που είχαν μείνει από τη δεύτερη ημέρα. Την τέταρτη ημέρα έπιασε τα υπόλοιπα οκτώ ποντίκια που είχαν μείνει από την τρίτη ημέρα. Πόσα ποντίκια υπήρχαν αρχικά; (Κατ.34/Νο.676)

Πηγή:http://mathefarm

Λύση

Αρχικά υπήρχαν 27 ποντίκια. Η γάτα τη πρώτη ημέρα έπισε 9 ποντίκια, τη δεύτερη ημέρα έπιασε 6 ποντίκια, τη τρίτη ημέρα έπιασε 4 ποντίκια και τη τέταρτη ημέρα έπιασε τα υπόλοιπα 8. Έστω «π» τα ποντίκια που υπήρχαν στην αρχή. Βάσει των δεδομένων της εκφωνήσεως του προβλήματος έχουμε: α)Τη πρώτη ημέρα έπιασε το 1/3 οπότε έμειναν υπόλοιπα: π–(π/3) = (3*π-π)/3 = 2*π/3 ποντίκια β)Τη δεύτερη ημέρα έπιασε το 1/3 από τα υπόλοιπα: (2*π/3)*1/3 =2*π/9 ποντίκια και μένουν υπόλοιπα: (2*π/3)-(2*π/9)= [(3*2*π)-2*π]/9 = (6*π-2*π)/9 = 4*π/9 ποντίκια. γ)Τη τρίτη ημέρα έπιασε το 1/3 από τα υπόλοιπα: (4*π/9)*1/3=4*π/27 ποντίκια και μένουν υπόλοιπα: (4*π/9)-(4*π/27)=[(3*4*π)-4*π]/27=(12*π-4*π)/27=8*π/27 ποντίκια δ)Επειδή, βάσει της εκφωνήσεως του προβλήματος, τη τέταρτη ημέρα επίασε τα υπόλοιπα 8 που είχαν μείνει, έχουμε τη εξίσωση: 8*π/27=8 --> 8*π=8*27 --> π=(8*27)/8 --> π=27 ποντίκια. Επαλήθευση: α)π/3 --> 27/3= 9 ποντίκια. β)2*π/9 --> (2*27)/9 --> 54/9= 6 ποντίκια γ)4*π/27 --> (4*27)/27 --> 108/27= 4 ποντίκια. δ) 8*π/27 --> (8*27)/27 --> 8 ποντίκια. Άρα έπιασε συνολικά: 9 + 6 + 4 + 8 = 27 ποντίκια ο.ε.δ.

Rebus No.163 (13)

Λύση

Σωματοφύλακας [Σωμα(ανθρώπινο)-το-φύλακας(άγγελος)]

Η Απόσταση

Μία κατοικίδια γάτα έφυγε κάποτε από το σπίτι της με ταχύτητα τρία χιλιόμετρα την ώρα. Ξαφνικά, θυμήθηκε ότι ήταν ώρα για το βραδινό και έτσι βιάστηκε να γυρίσει πίσω με ταχύτητα διπλάσια από πριν. Συνολικά έλειπε για δεκαπέντε λεπτά. Πόσο μακριά είχε πάει από το σπίτι της; (Κατ.34/Νο.675)

Πηγή: http://mathefarm

Λύση

Η απόσταση που διήνησε από το σπίτι μέχρι το σημείο "x" ήταν 500μ. ή 0,5χιλιόμετρο. Έστω «S» η απόσταση σε χιλιόμετρα που διένυσε η γάτα προτού αποφασίσει να γυρίσει πίσω και «t1» ώρες ο χρόνος που έκανε για να την διανύσει με ταχύτητα 3 χλμ/ώρα .Κατόπιν, γύρισε πίσω στην αφετηρία διανύοντας την ίδια απόσταση με διπλάσια ταχύτητα απ’ ότι ήταν η ταχύτητα όταν πήγε στο σημείο «x» σε χρόνο t2 ώρες. Βάσει του τύπου της ευθύγραμμης ομαλής κίνησης έχουμε: S=υ*t1 και S=υ*t2 Επειδή διήνησε την ίδια απόσταση έχουμε: S1=S2 --> υ*t1=2*υ*t2 --> 3*t1=3*2*t2 --> 3*t1=6*t2 --> t1=(6*t2 )/3 --> t1=2*t2 (1) Ο συνολικός χρόνος που χρειάσθηκε για να πάει και να γυρίσει είναι: t1+t2 =15/60 ώρες (2) Αντικαθιστού με την (1) στη (2) κι’ έχουμε: t1+t2 =15/60 --> 2*t2+t2=15/60 --> 3*t2=15/60 Απλοποιούμε το κλάσμα στο δεύτερο μέλος με το 15 κι’ έχουμε: 3*t2=15/60 --> 3*t2=1/4 --> t2=1/4*3 --> t2=1/12 ώρες (3) Αντικαθιστούμε τη (3) στην (1) κι’ έχουμε: t1=2*t2 --> t1=2*(1/12) --> t1=2/12 --> t1=1/6 ώρες (4) Επομένως η γάτα διήνησε μια απόσταση από το σπίτι μέχρι το σημείο «x»: S=υ*t1 --> S=3*(1/6) --> S=3/6 --> S=1/2=0,5χιλιόμετρα ή 500μέτρα. Επαλήθευση: S(ο)=υ*t1=2*υ*t2 --> S(ο)=3*(1/6)=2*3*(1/12) --> S(ο)=3/6=6/12=1/2=0,5χλμ. t1+t2 =15/60 --> 1/6+1/12=15/60 --> (2+1)/12=15/60 --> 3/12=15/60 --> 1/4=1/4

Rebus No.162 (9)

Λύση

Καρναβάλι [Καρνα(γιο*)βαλι(Voldemar Väli**)] *Καρνάγιο ή Ταρσανάς, μικρό ναυπηγείο. ** Βολντεμάρ Βάλι (Voldemar Väli). (10-1-1903 Kuressaare – 13- 4-1997 Stockholm)). Εσθονός παλαιστής της ελληνορωμαϊκής. Ολυμπιονίκης το 1928 στα 62κιλά και 3ος το 1936, στα 61-66κιλά, ενώ το 1924 ήταν 8ος στα 62κιλά. Πρωταθλητής Ευρώπης το 1926 και 1926 στα 62κιλά και 2ος το 1930 στα 66κιλά.. Πέθανε στη Στοκχόλμη στις 13 Απριλίου 1997.

Το Κυνηγητό

‘Ενας σκύλος κυνηγά μια αλεπού, η οποία προηγείται απο το σκύλο κατά 84 πηδήματά της. ‘Οταν ο σκύλος κάνει 6 πηδήματα, η αλεπού κάνει 10, αλλά 4 πηδήματα του σκύλου ισοδυναμούν με 9 της αλεπούς. Μετά από πόσα πηδήματά του ο σκύλος θα φτάσει την αλεπού; (Κατ.6/No.10)

Πηγή:http://www.rhodes.aegean.gr/ptde/personel/chionidou/Problems%20gia%20Efarmoges%20Epilyshw%20kai%20Didaskalias%20%20G%20Fas%20tekmhrio%203-1i.pdf

Λύση

Ο σκύλος θα φθάσει την αλεπού μετά από 144 πηδήματα. Έστω ότι ο σκύλος θα φθάσει την αλεπού μετά "α" πηδήματα του. Αλλά κατά το διάστημα αυτό η αλεπού, εκτός των 84 πηδημάτων της, που προπορεύεται του σκύλου, θα έχει διανύσει και (10α)/6 πηδήματα ακόμη, διότι: Όταν ο σκύλος κάνει 6 πηδήματα η αλεπού κάνει 10 πηδήματα. Όταν ο σκύλος κάνει 1 πήδημα η αλεπού κάνει 10/6 πηδήματα. Όταν ο σκύλος κάνει "α" πήδημα η αλεπού κάνει (10α)/6 πηδήματα. Συνολικά η αλεπού έχει κάνει [84+(10α)/6] πηδήματα. Μετατρέπουμε τα πηδήματα της αλεπούς σε πηδήματα σκύλου: Τα 9 πηδήματα της αλεπούς ισοδυναμούν με 4 πηδήματα του σκύλου. Το 1 πήδημα της αλεπούς ισοδυναμεί με 4/9 πηδήματα του σκύλου. Τα [84+(10α)/6] πηδήματα. της αλεπούς ισοδυναμούν με (4/9)*[84+(10α)/6] πηδήματα. Επειδή θα συναντηθούν σε κάποιο σημείο θα έχουν διανύσει την ίδια απόσταση. Επομένως έχουμε την εξίσωση: α =(4/9)*[84+(10α)/6] --> α=(4/9)*[(84*6)+10α]/6 --> α=4*(504+10α)/9*6 --> α=(2.016+40α)/54 --> 54α=2.016+40α --> 54α-40α=2.016 --> 14α=2.016--> α=2.016/14 --> α=144

Η Πισίνα

Μια βρύση γεμίζει μια πισίνα με νερό σε «α» ώρες. Μια δεύτερη αδειάζει τη πισίνα σε «β» ώρες. Εάν η πισίνα είναι άδεια και ανοίξουμε και τις δύο βρύσες συγχρόνως, σε πόσες ώρες θα γεμίσει η πισίνα με νερό; (Κατ.34/Νο.674)

Πηγή:http://www.rhodes.aegean.gr/ptde/personel/chionidou/Problems%20gia%20Efarmoges%20Epilyshw%20kai%20Didaskalias%20%20G%20Fas%20tekmhrio%203-1i.pdf

Λύση

Λύση του Ε. Αλεξίου. Η πισίνα θα γεμίσει με νερό σε α*β/(β-α) ώρες. Σε μια ώρα η μία βρύση γεμίζει (1/α) της πισίνας με νερό και η άλλη βρύση αδιάζει το (1/β) της πισίνας. Συνεπώς σε 1 ώρα γεμίζει το 1/α -1/β της πισίνας =(β-α)/(α*β), άρα πρέπει το "β" να είναι μεγαλύτερο του "α", γιατί αλλιώς η πισίνα δεν θα έχει ούτε σταγόνα νερό. Συνεπώς η πισίνα θα γεμίσει σε: 1/[(β-α)/(α*β)]=α*β/(β-α) ώρες.

Ο Ιδιόρρυθμος Δωρητής

Ένας παράξενος μαθηματικός, θέλοντας να κάνει δώρα σε πέντε φίλους του, τούς αρίθμησε κατά σειρά από το 1 έως το 5 κι’ έδωσε στο καθένα τους από μία μάρκα. Η μάρκα του πρώτου είχε τον αριθμό 5, του δευτέρου τον αριθμό 25, του τρίτου τον αριθμό 125, του τέταρτου τον αριθμό 625 και του πέμπτου τον αριθμό 3.125. Στη συνέχεια τους παρουσίασε τα πέντε δώρα του, τα οποία είχε αριθμήσει, επίσης  με τους αριθμούς από το 1 έως το 5. Μετά απ’ όλη αυτή τη διαδικασία τους είπε  να διαλέξει ο καθένας τους ένα  από τα πέντε αριθμημένα δώρα και να πολλαπλασιάσουν τον αριθμό του εκλεγέντος δώρου επί τον αριθμό της μάρκας τους. Μετά και από τη διαδικασία αυτή ο μαθηματικός πρόσθεσε τα προκύψαντα γινόμενα και βρήκε ως τελικό άθροισμα 9.615. Ισχυρίσθηκε δε, ότι μπορεί να βρει ποιο δώρο διάλεξε ο καθένας. Εσείς τι λέτε, τα κατάφερε ο ιδιόρρυθμος μαθηματικός να βρει πιο δώρο διάλεξε ο καθ’ ένας από τους φίλους του; (Κατ.34/Ν.673)
Πρόβλημα του Αββά Huelle.

Λύση

Ο «α» πήρε το δώρο Νο.3, ο «β» πήρε το δώρο Νο.4, ο «γ» πήρε το δώρο Νο.1, ο «δ» πήρε το δώρο Νο.5, ο «ε» πήρε το δώρο Νο.2 Έστω «α», «β», «γ», «δ» και «ε» οι αριθμοί των δώρων, βάσει των δεδομένων της εκφωνήσεως του προβλήματος έχουμε: α)5α+25β+125γ+625δ+3.125ε=9.615 Απλοποιούμε το πρώτο μέλος της εξίσωσης με το 5 κι’ έχουμε: α+5β+25γ+125δ+625ε=1.923 Οι τέσσερεις τελευταίοι όροι του πρώτου μέλους της ανωτέρω εξίσωσης διαιρούνται δια του 5, οπότε η τιμή του "α" είναι το υπόλοιπο της διαιρέσεως του 1.923 διά του 5, που είναι το 3 (1.923mod5). Άρα α=3 . β)5β+25γ+125δ+625ε=1920 Απλοποιούμε το πρώτο μέλος της εξίσωσης με το 5 κι’ έχουμε: β+5γ+25δ+125ε=384 Οι τρεις τελευταίοι όροι του πρώτου μέλους της ανωτέρω εξίσωσης διαιρού- νται δια του 5, οπότε η τιμή του "β" είναι το υπόλοιπο της διαιρέσεως του 384 διά του 5, που είναι το 4 (384mod5). Άρα β=4 . γ)5γ+25δ+125ε=380 Απλοποιούμε το πρώτο μέλος της εξίσωσης με το 5 κι’ έχουμε: γ+5δ+25ε=76 Οι δύο τελευταίοι όροι του πρώτου μέλους της ανωτέρω εξίσωσης διαιρούνται δια του 5, οπότε η τιμή του "γ" είναι το υπόλοιπο της διαιρέσεως του 76 διά του 5, που είναι το 1(76mod5). Άρα γ=1 . δ)5δ+25ε=75 Απλοποιούμε το πρώτο μέλος της εξίσωσης με το 5 κι’ έχουμε: δ+5ε=15 Οι τελευταίος όρος του πρώτου μέλους της ανωτέρω εξίσωσης διαιρείται διά του 5, οπότε η τιμή του "δ" είναι ο διαιρέτης του15, που είναι ο 5 (15mod5). Άρα δ=5 . ε)5ε=10 --> ε =10/5 . Άρα ε = 2 Επαλήθευση: 5α+25β+125γ+625δ+3.125ε=9.615 --> (5*3)+(25*4)+(125*1)+(625*5)+(3.125*2)=9.615 --> 15+100+125+3.125+6.250=9.615 ο.ε.δ.

Rebus No.161 (6)

Λύση

Χαρέμι [Χα(Χρηματιστήριο Αθηνών)ρεμι(Loic Remy=ποδοσφαιριστής)]

Το Χαρέμι

Ένας Άραβας είχε μία  σύζυγο λιγότερη από όσες είχε ο μεγαλύτερος αδελφός του. Ο μεγαλύτερος αδελφός του είχε μία σύζυγο λιγότερη από όσες είχε ο Σεΐχης. Ο μικρότερος αδελφός του Σεϊχη είχε τις μισές συζύγους από όσες είχε ο Σεΐχης. Πόσες συζύγους είχε ο καθένας; (Κατ.34/Νο.672)

Πηγή:http://mathefarm

Λύση

Λύση του "Ανώνυμος". Αν μας ενδιαφέρει να βρούμε τις λιγότερες δυνατές γυναίκες που μπορεί να υπήρχαν και πόσες είχε ο καθένας, τότε ο πρώτος Άραβας έχει 2 γυναίκες, ο μεγαλύτερος αδελφός του 3 και ο Σεΐχης 4. Ο μικρότερος αδελφός του Σεΐχη έχει 2 και ταυτίζεται με τον πρώτο Άραβα καθώς μπορεί όλοι να είναι αδέλφια. Οι ελάχιστες γυναίκες είναι λοιπόν 9. Συμπλήρωση από Papaveri. Επειδή το πρόβλημα δεν διευκρινίζει, εάν όλοι είναι αδέλφια, δεχόμαστε τελικά ότι το σύνολο των συζύγων είναι 11.

Οι Αριθμοί

Οι αριθμοί στο πάνω μέρος του κάθε σχήματος έχουν μία σχέση που προσδιορίζει τον κόκκινο αριθμό. Να βρείτε τους αριθμούς που λείπουν στα επόμενα σχήματα. (Κατ.2/Νο.159)

Πηγή:http://mathefarm

Λύση

Α)Στο ορθογώνιο «Α», στο άθροισμα των δύο αριθμών προσθέτουμε τον αριθμό 1. Β)Στο ορθογώνιο «Β» το άθροισμα των δύο αριθμών το διαιρούμε με το αριθμό 2. Γ)Στο ορθογώνιο «Γ» το γινόμενο των δύο αριθμών το διαιρούμε με τον αριθμό 3. Α)32+15=47+1=48, 12+13=25+1=26, 15+29=44+1=45(?) Β)32+20=52:2=26, 12+18=30:2=15, 8+10=18:2=9(?) Γ)8*9=72:3=24, 3*12=36:3=12, 9*7=63:3=21(?)

Rebus No.160 (9)

Λύση

Πολύγυρος(Χαλκιδικής)[Πολη(Κωνσταντινούπολη*)γυρος**] *Ο Ναός Αγίων Σέργιου και Βάκχου ή αλλιώς το Τζαμί της Μικρής Αγια-Σοφιάς (Küçük Ayasofya Camii) είναι δίπλα στην Αγία Σοφία και διαθέτει μια σκαλιστή επιγραφή στα ελληνικά με τους ιδρυτές του ναού. **Γύρος (Ντόνερ-Κεμπάπ- Τουρ. Döner Kebap) ονομάζεται το έδεσμα που αποτελείται από κομμάτια χοιρινού κρέατος από διάφορα μέρη του ζώου. Το νοστιμότερο γύρο τον κάνει κρέας από το λαιμό του χοίρου. Ονομάζεται από την ελληνική γύρα ή αλλιώς περιστροφή που κάνει το κρέας στην κατακόρυφη μεταλλική σούβλα που περνιέται για να ψηθεί γύρω από τον άξονά της, με τη φωτιά στη μια πλευρά. Ο γύρος φτιάχνεται και με κιμά - όπως το γνωστό κεμπάπ - αλλά και με κρέας κοτόπουλου. Προσφέρεται τυλιγμένος σε πίτα (άζυμο ψωμί), αλλά και ως μερίδα. Σερβίρεται με διάφορες σαλάτες - χαρακτηριστικότερη το τζατζίκι - ντομάτα, κρεμμύδι και τηγανητές πατάτες. Σήμερα στην Ελλάδα ο γύρος με κιμά έχει απαγορευθεί με σχετική αγορανομική διάταξη λόγω των υγειονομικών παραβάσεων που είχαν σημειωθεί Ιστορία: Τα μικρομάγαζα που άνοιξαν το 1922-1923 οι πρόσφυγες από τη Σμύρνη και την Κωνσταντινούπολη μετά τον πόλεμο εξαπλώθηκαν σε κάθε γωνιά της Ελλάδας. Οι συνταγές του γύρου εξαπλώθηκαν με την μετανάστευση ως την Αμερική και την Αυστραλία. Σήμερα, μεγάλες εταιρίες εστίασης, όπως τα Goody's, τα everest (Πολίτικο) και τα McDonald's προσφέρουν κάποια παραλλαγή γύρου στο μενού τους. Στην Γερμανία και την Γαλλία το ντόνερ αποτελεί εδώ και χρόνια αγαπημένο έτοιμο φαγητό, ενώ και ο χοιρινός γύρος των Ελλήνων αποτελεί γνωστό φαγητό. Νέες γεύσεις προστέθηκαν, ενώ υπάρχουν πλέον και ο "πράσινος ή οικολογικός γύρος" και ο "παιδικός γύρος". Στην Αθήνα και τη Θεσσαλονίκη πωλείται ακόμη και μέσω του διαδικτύου. Παρόμοια Φαγητά με το Γύρο: Το αραβικό φαγητό «shawarma» και το μεξικάνικο «tacos al pastor» είναι όλα παρόμοια με τον γύρο, και όλα προέρχονται από το Τουρκικό Ντόνερ Κεμπάπ το οποίο δημιουργήθηκε στην πόλη Προύσα τον 19ο αιώνα. Το ντόνερ κεμπάπ αποτελείται από αρνίσιο ή μοσχαρίσιο κρέας ή κοτόπουλο, ωστόσο στην Ελλάδα επικράτησε παραλλαγή με χοιρινό, αφού οι Χριστιανοί μπορούν να καταναλώσουν αυτό το κρέας. Στα Αραβικά Εμιράτα βάζουν αντί για τζατζίκι ψιλοκομμένο φιστίκι, ενώ ακόμα και σήμερα στην Κρήτη χρησιμοποιούν γιαούρτι. Ο γύρος είναι ένα από τα σημαντικότερα εδέσματα που έχει σκοπό να δοκιμάσει ο τουρίστας κατά την επίσκεψη του στην Ελλάδα, μαζί με το μουσακά και το σουβλάκι. Tο Ντόνερ Κεμπάπ (Τουρ. Döner Kebap), που σημαίνει «σούβλα που γυρίζει», είναι η ονομασία ενός τουρκικού φαγητού στο οποίο χρησιμοποιείται αρνίσιο κρέας, μοσχαρίσιο ή κοτόπουλου. Παραλλαγές του ντόνερ περιλαμβάνουν το "Σουτζούκ Ντόνερ" δηλ. ντονέρ από σουτζούκι και το "Μπαλίκ Ντόνερ", ντόνερ που παρασκευάζεται με φιλέτο ψαριού. Αντίστοιχα μεσογειακά και μεσανατολίτικα φαγητά είναι το σαβαρμά (shawarma) και ο γύρος. Το ντόνερ αποτελεί σήμερα ένα από τα αγαπημένα έτοιμα φαγητά στον κόσμο. Ιστορία: Το σημερινό ντόνερ προέρχεται από το παλαιότερο ολτού κεμπάπ (Oltu Kebap). Το Ολτού είναι μια μικρή πόλη κοντά στο Ερζερούμ στην Τουρκία. Στην αρχική μορφή του, το κρέας ψηνόταν οριζόντια και τα κομμάτια κρέατος κόβονταν πιο χοντρά. Η σημερινή μορφή έγινε τον 19ο αιώνα στην Προύσα. Σε πολλές πόλεις της Τουρκίας η αρχική μορφή του σερβίρεται ακόμα σε εστιατόρια. Σήμερα, το ντόνερ σερβίρεται σαν σάντουιτς μέσα σε τουρκική πίτα. Ο τρόπος σερβιρίσματος του ντόνερ με σαλάτα και σως δημιουργήθηκε από Τούρκους μετανάστες του Βερολίνου το 1971, ώστε να γίνει το γεύμα πιο ελκυστικό για τους Γερμανούς πελάτες. Το ντόνερ είναι από την δεκαετία του 1980 το πιο δημοφιλές έτοιμο φαγητό στην Γερμανία.

Ο Αριθμός

Με ποιον αριθμό πρέπει ν’ αντικαταστήσουμε το ερωτηματικό; Ο ίδιος λογικός κανόνας ισχύει και στις τρεις στήλες.(Κατ.2/No.158)

Πηγή:http://mathefarm

Λύση

Λείπει ο αριθμός 24 ή "Ο αριθμός των γραμμάτων του αλφαβήτου.", όπως πολύ ωραία το διατύπωσε ο «Ανώνυμος». Σε κάθε στήλη διαιρούμε το δεύτερο αριθμό με το πρώτο αριθμό και το πηλίκο το πολλαπλασιάζουμε με το τρίτο αριθμό όπου προκύπτει ο τέταρτος αριθμός. Α)8:4=2*16=32. Β)10:5=2*20=40. Γ)12:6=2*?=48 --> ?=48:2=24 --> 12:6=2*24(?)=48.

Ο Αριθμός

Παρατηρώντας τους τρεις πρώτους κύκλους, να βρεθεί ποια σχέση συνδέει τους τρεις αριθμούς. Με τη βοήθεια της σχέσης αυτής, να βρείτε τον αριθμό που λείπει στον τέταρτο κύκλο.(Κατ.2/Νο.157)

Πηγή:http://mathefarm

Λύση

Λείπει ο αριθμός 3. Σε κάθε κύκλο προσθέτουμε τους δύο αριθμούς που βρίσκονται στα δύο τεταρτημόρια και το άθροισμα το πολλαπλασιάζουμε με τον αριθμό 2, όπου προκύπτει ο αριθμός στο ημικύκλιο. Α)(5+4)*2=9*2=18. Β)(12+8)*2=20*2=40. Γ)(3+9)*2=12*2=24. Δ)(4+?)*2=14 --> (4+?)=14/2 --> (4+?)=7 --> ?=7-4=3 --> (4+3)*2=7*2=14

Rebus No.159 (9)

Λύση

Αστροπύλη [Αστρο(ς)(Η γοργόνα Σθενώ* στο Αστρος Κυνουρίας)πυλη(Υψηλή Πύλη**)] * Η Σθενώ, στην ελληνική μυθολογία, ήταν η μεγαλύτερη από τις Γοργόνες. Η κόρη του Φόρκυς και Κητώ, γεννήθηκε στις σπηλιές κάτω από τον Όλυμπο. Αυτή και η αδελφή της η Ευρυάλη ήταν αθάνατες, ενώ η τρίτη αδελφή, Μέδουσα, ήταν θνητή. Από τις τρεις Γοργόνες, ήταν γνωστό ότι είναι η πιο ανεξάρτητη και άγρια, έχει σκοτώσει περισσότερους άνδρες από ό, τι και οι δύο αδελφές της μαζί. Η Μέδουσα ήταν καταραμένη από την Αθηνά, επειδή ο Ποσειδώνας την βίασε στο ναό της Αθηνάς. Η Αθηνά ήταν πολύ θυμωμένη, αλλά όχι με τον Ποσειδώνα. Ως ένας ισχυρός αρσενικός θεός, αυτό θα πρέπει να αναμένεται από αυτόν. Στα μάτια της Αθηνάς, η Μέδουσα άξιζε να τιμωρηθεί. Ως τιμωρία,την μετέτρεψε σε ένα φοβερό τέρας. Η Σθενώ τείνει να απεικονίζεται ως μία λεπτή γοργόνα με κόκκινα φίδια γύρω από το κεφάλι της αντί για τα μαλλιά. ** Ο όρος Υψηλή Πύλη ή Μεγάλη Πόρτα, αρχικά σήμαινε την πύλη της Σουλτανικής σκηνής που ήταν η μεγαλύτερη απ΄ όλες τις άλλες. Μετά την κατάληψη της Κωνσταντινούπολης ονομάσθηκε έτσι το Σουλτανικό Ανάκτορο. Αργότερα η Υψηλή Πύλη περιορίστηκε μόνο για το τμήμα εκείνο του Ανακτόρου όπου στέγαζε το γραφείο του Μεγάλου Βεζίρη και των υπηρεσιών του, αναφερόμενο πλέον στην κυβέρνηση του Οθωμανικού κράτους.

Ο Αριθμός

Ο δεύτερος, τρίτος και τέταρτος αριθμός σε κάθε σειρά βρίσκονται με μία απλή μεθοδολογία που εφαρμόζεται ξεκινώντας από τον πρώτο αριθμό της κάθε σειράς. Με το τρόπο αυτό να βρεθεί με ποιον αριθμό πρέπει ν’ αντικαταστήσουμε το ερωτηματικό. (Κατ.2/Νο.156)

Πηγή:http://mathefarm

Λύση

Λείπει ο αριθμός 14.Σε κάθε σειρά πολλαπλασιάζουμε τα ψηφία κάθε αριθμού και προκύπτει ο επόμενος αριθμός. Α)384 --> 3*8*4=96 --> 9*6=54 --> 5*4=20 --> 2*0=0, Β)624 --> 6*2*4=48 --> 4*8=32 --> 3*2=6, Γ)579 --> 5*7*9=315 --> 3*1*5=15 --> 1*5=5, Δ)739 --> 7*3*9=189 --> 1*8*9=72 --> 7*2=14(?) --> 1*4=4

Rebus No.158 (10)

Λύση

ΠΛΑΝΗΤΑΡΙΟ [Πλάνη(ξυλουργικό εργαλείο για τη λείανση του ξύλου )-τάριο(Tario Fuller, παίκτης ράγκμπι)]

Οι Αριθμοί

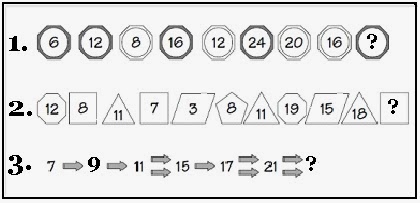
Σε κάθε μία από τις τρεις ακολουθείες που ακολουθούν υπάρχει ένας λογικός κανόνας για τον αριθμό που μπαίνει σε κάθε θέση. Ποιος είναι ο επόμενος αριθμός σε κάθε μία από τις τρεις ακολουθείς; (Κατ.2/Νο.155)

Πηγή:http://mathefarm

Λύση

Λύση του batman1986: 1. Παρατηρώ πάλι κάποια αλληλουχία όταν είναι 2 συνεχόμενα σκούρα έχουμε διπλασιασμό του αριθμού του 1ου. Όταν είναι ασπρο-σκούρο πάλι διπλασιασμό Όταν σκούρο-άσπρο αφαιρούμε 4 Άρα σ αυτή την περίπτωση αφού έχουμε άσπρο σκούρο τότε λείπει το 32. 2. Εδώ είναι εμφανές ότι ο επόμενος αριθμός προκύπτει είτε προσθέτοντας είτε αφιαρώντας από τον προηγούμενο τον αριθμό των πλευρών του σχήματος στο οποίο είναι μέσα (ο επόμενος) Το αν θα προσθέσουμε η αφαιρέσουμε εξαρτάται από την αλληλουχία των σχημάτων Απ ότι βλέπουμε αν μετά το τρίγωνο έχουμε τετράγωνο τότε αφαιρούμε Άρα λείπει 18-4(εφόσον ο άγνωστος είναι μέσα σε τετράγωνο)=14. 3. Εδώ βλέπουμε ότι όταν ακολουθεί ένα βέλος μετά από κάθε αριθμό έχουμε αύξηση κατά 2 ενώ όταν ακολουθούν 2 βέλη έχουμε αύξηση κατά 4 Άρα αυτός που λείπει είναι 21+4=25 Λύση του SW: ΣΕΙΡΑ 1. Έχουμε σκούρου και ανοιχτού χρώματος κύκλους. Μετά τον πρώτο όρο όταν βρίσκουμε σκούρο κύκλο γράφουμε στο εσωτερικό του το διπλάσιο αριθμό από τον προηγούμενο. Σε ανοιχτού χρώματος κύκλο αφαιρούμε 4 μονάδες από τον προηγούμενο κύκλο. Έτσι ο τελευταίος κύκλος είναι σκούρου χρώματος, διπλασιάζουμε τον προηγούμενο αριθμό και γράφουμε σαν συνέχεια τον αριθμό 32. ΣΕΙΡΑ 2. Το πλήθος των πλευρών κάθε σχήματος συμβολίζουν τον αριθμό που πρέπει να προσθέσουμε η να αφαιρέσουμε από τον προηγούμενο αριθμό. Στα τετράπλευρα αφαιρούμε ενώ σε όλα τα υπόλοιπα σχήματα προσθέτουμε τον προηγούμενο αριθμό. Το τελευταίο σχήμα είναι τετράπλευρο, άρα αφαιρούμε από το προηγούμενο 4 και πρέπει να γράψουμε τον αριθμό 14. ΣΕΙΡΑ 3. Κάθε βέλος συμβολίζει τον αριθμό 2. Ένα βέλος προσθέτουμε 2 στον επόμενο όρο της σειράς, με δύο βέλη 4. Έτσι έχουμε 2 βέλη στον τελευταίο όρο της σειράς που πρέπει να είναι ο 25. Πρόσθετη λύση για την πρώτη ακολουθεία: Στην πρώτη ακολουθεία υπάρχουν τρία λάθη: Το πρώτο οκτάγωνο πρέπει να είναι ανοικτού χρώματος. Το οκτάγωνο με τον αριθμό 16 πρέπει να είναι σκούρου χρώματος. Το οκτάγωνο με το ερωτηματικό πρέπει να είναι ανοικτού χρώματος. Οπότε η λύση είναι ένας άλλος αριθμός: 6*2=12-4=8*2=16-4=12*2=24-4=20*2=40-4=36(?)

Rebus No.157 (13,11,7)

Λύση

Διαγαλαξιακός Διαστημικός Σταθμός [Δια(νησίδα*)γαλαξια**(ς)κος(Κως είναι νησί του Αιγαίου) Διαστημ(α)ικός(Κως είναι νησί του Αιγαίου) Σταθμός***] *Η Δία είναι νησίδα του Κρητικού Πελάγους και βρίσκεται βόρεια του Ηρακλείου από το οποίο απέχει 7 ν.μ.. Έχει έκταση 11,909 Km2 μέγιστο μήκος 5χλμ. και πλάτος 3χλμ[1]. Διοικητικά ανήκει στον δήμο Χερσονήσου Ηρακλείου, στην τοπική κοινότητα Ελιάς Ηρακλείου και σύμφωνα με την απογραφή του 2001 είναι ακατοίκητη. **Ο σπειροειδής γαλαξίας Μ100 ανήκει στο σμήνος γαλαξιών της Παρθένου ( Virgo cluster) και είναι ένας από τα λαμπρότερα μέλη. Στον κατάλογο Messier υπάρχουν 16 γαλαξίες του σμήνους και συνολικά περίπου 2000 γαλαξίες. Η απόσταση του είναι 60.000 έτη φωτός. ***Διεθνής Διαστημικός Σταθμός (ISS) -MIR (Ρωσικός)

Η Ισορροπία

Με πόσα σταθμά πρέπει ν’ αντικαταστήσουμε το ερωτηματικό; (Κατ.9Α΄/Νο.22)

Πηγή:http://eisatopon.blogspot.gr/2012/02/blog-post_9302.html

Λύση

Έστω M=μπλε, Κ=κόκκινο, Π=πράσινο, Γ=γκρι η ονομασία των σταθμών. Βάσει των ανωτέρω δεδομένων έχουμε: 2(Μ+Κ)=Μ+Π (1), 2Γ=Κ+Γ+Π (2), 2(Κ+Κ)=Μ+Γ (3), 2Μ=Κ+? (4). Από την (1) συνάγουμε ότι: 2(Μ+Κ)=Μ+Π --> 2Μ+2Κ=Μ+Π --> Μ=Π-2Κ (5). Από τη (2) συνάγουμε ότι: 2Γ=Κ+Γ+Π --> 2Γ-Γ=Κ+Π --> Γ=Κ+Π --> -Κ=Π-Γ (6). Από τη (3) συνάγουμε ότι: 2(Κ+Κ)=Μ+Γ --> 2Κ+2Κ=Μ+Γ --> 4Κ=Μ+Γ --> Μ=4Κ-Γ (7). Προσθέτουμε κατά μέλη τη (5) και την (7) κι’ έχουμε: 2Μ=4Κ-2Κ+Π-Γ --> 2Μ=2Κ+Π-Γ (8). Αντικαθιστούμε το (Π-Γ) με -Κ (6). 2Μ=2Κ+Π-Γ --> 2Μ=2Κ-Κ --> 2Μ=Κ (9). Άρα η ζυγαριά ισορροπεί, χωρίς ν’ αντικαταστήσουμε το ερωτηματικό με κάποιο από τα σταθμά.

Σταυρόλεξο Νο.3

ΟΡΙΖΟΝΤΙΑ

1.       Ο χώρος των πιστών, ο οποίος βρίσκεται μεταξύ του Ιερού και του Νάρθηκα.

2.       Δήμος του Πειραιά.

3.       Ένας κώδικας – Από του Άδωνη… φύτρωσε η ανεμώνη – Νότα μουσικής του Ευρωπαϊκού πενταγράμμου.

4.       Στερεώνει τα μαλλιά – Ο αερομεταφορέας μας. (αρχικά) –
«Ή επί … ή επί ταν»,έλεγαν οι Σπαρτιάτισσες μητέρες στα παιδιά τους
όταν τους έδιναν τις ασπίδες τους. (αντ.)

5.       Κινέζικη ονομασία του Βιετ-Ναμ – Το μπαστούνι της τράπουλας.

6.       Σπουδαίας σημασίας όργανο του ανθρώπου. – Γυναικείο όνομα. (αντ.)

7.       Περίπατος νηπίων – Άηχη μάσα – Άλλο σπουδαίο όργανο του ανθρώπου. (καθ. αντ. πληθ.)

8.       Άρθρο (πληθ.) – Παιγνίδι της τράπουλας – Υποθετικό.

9.       Νύμφη των υδάτων, μια από τις πενήντα κόρες του Δαναού. (μυθ.)

10.    Αυτός που ανήκει στο ΝΑΤΟ.

±.±.±

ΚΑΘΕΤΑ

1.       Πόλη της Μεσσηνίας, ξακουστή για τις ελιές της.

2.       Πήλινο ή υάλινο σκεύος για υγρά.

3.       Παλιά αρχικά της ΕΛ-ΑΣ – Πρόθεση – Μόριο.

4.       Γυναίκα πανέμορφη (μτφ.) – Νότα μουσικής του Ευρωπαϊκού πενταγράμμου – Ισοπαλία σκακιστών που γίνεται από αναγκαστική κίνηση.

5.       Σύνορο – Όχι ζυγό.

6.       Προβατοκάμηλος, αλλά και μέρος του ονόματος θρησκευτικού ηγέτη – Τηλεοπτικό κανάλι.

7.       …Σούμακ, το αηδόνι των Άνδεων – Νότα της βυζαντινής μουσικής – Χαϊδευτικό του Προέδρου των Η.Π.Α. Ντουάϊτ Αϊζενχάουερ.

8.       Η ψυχή των αρχαίων Αιγυπτίων (μυθ.) – Βιβλικό βουνό – Ιρλανδός θεατρικός συγγραφέας και πεζογράφος.(1856-1950)

9.       Χωρίς αυτή δεν μπορεί να πραγματοποιηθεί ένα αγώνισμα.

10.    Καλιγώνω.

±.±.±

(c. de g.2007^® No.3)

Διαβάστε περισσότερα »

Rebus No.156 (8)

Λύση

Παράταξη [Παρα(ς*)ταξη(τάξη σχολείου)] *Ασημένιος παράς που υποδιαιρούνταν σε 3 ακτσέ του Μουσταφά Γ' (1757-1774).

Η Ισότητα

Με πόσους κύκλους πρέπει ν’ αντικαταστήσουμε το ερωτηματικό; (Κατ.9Α΄/Νο.21)
Πηγή:http://eisatopon.blogspot.gr/2012/02/blog-post_986.html

Λύση

Το ερωτηματικό πρέπει ν’ αντικατασταθεί απο 5 κύκλους. Έστω «α» το τετράγωνο, «β» ο κύκλος, «γ» το τρίγωνο, και «δ» ο ρόμβος. Βάσει των ανωτέρω έχουμε: α+β=γ (1), β+δ=α (2), 2γ=3δ (3), α=? (4). Αντικαθιστούμε την (1) στη (3) κι’ έχουμε: 2γ=3δ --> 2*(α+β)=3δ --> δ=2*(α+β)/3 (5) Αντικαθιστούμε τη (5) στη (2) κι’ έχουμε: β+δ=α--> α=β+2*(α+β)/3 --> α=[3β+2*(α+β)]/3 --> 3α=3β+2α+2β --> 3α-2α=5β --> α=5β (6) Επαλήθευση: α+β=γ --> 5β+β=γ --> γ=6β, β+δ=α--> 5β=β+δ --> δ=5β-β --> δ=4β, 2γ=3δ --> 2*6β=3*4β --> 12β=12β, α=? --> α=5β ο.ε.δ.