- (α)Σε ποια θέση θα βρίσκεται το σημείο "A" μετά από τις τρεις περιστροφές;
- (β)Πόσο θα είναι το μήκος της διαδρομής που θα έχει διανύσει; (Κατ.27)
Λύση
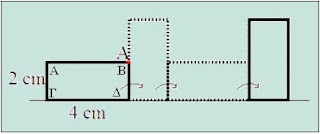
Μετά την τρίτη περιστροφή το σημείο «Α» βρίσκεται στην επάνω αριστερή γωνία με την επισήμανση «Β» (Βλέπε ανωτέρω σχήμα).(1)Έστω ΑΒΓΔ η οριοθέτηση του ορθογωνίου, με «Β» η επισήμανση «Α».
1η περιστροφή: Έχουμε ΔΑΒΓ.
2η περιστροφή: Έχουμε ΓΔΑΒ.
3η περιστροφή: Έχουμε ΒΓΔΑ.
(2)Σε κάθε περιστροφή η διαδρομή αποτελείται από ένα τεταρτημόριο του κύκλου με ακτίνες έκαστου τεταρτημόριου 2εκ., 0εκ., και 4εκ. αντίστοιχα. Άρα η συνολική διαδρομή που θα διανύσει είναι:
π+0+2π=3π εκ.= 3*3,14159265=9,42477795εκ.=9,42εκ.
Λύση του μαθηματικού Κώστα Δόρτσιου:
Διαδρομή του σημείου «Α»
τοξ(ΜΕ)+τοξ(ΕΓ)=2π*2*(90ο/360ο)+2π*4**(90ο/360ο)=4π*(1/4)+8π*(1/4)=π+2π=3π εκ.
Μια πολύ ωραία περιστροφή εν κινήσει του μαθηματικού Κώστα Δόρτσιου μπορείτε να δείτε εδώ:
http://eisatopon.blogspot.gr/2016/05/blog-post_17.html
















2 σχόλια:
1. Πάνω αριστερά.
2. Σε κάθε περιστροφή η διαδρομή είναι τεταρτοκύκλιο και οι ακτίνες 2, 0 και 4 εκατοστά. Άρα η συνολική διαδρομή είναι π+0+2π=3π εκ.
@Ανώνυμος
Συγχαρητήρια! Η απάντησή σας είναι σωστή.
Δημοσίευση σχολίου